TL;DR
DES (Data Encryption Standard)DES: DES is a symmetric-key block cipher adopted in 1977 by the National Institute of Standards and Technology(NIST) and was initially created by an IBM team. Symmetric indicates that the cipher will use the same key to encrypt or decrypt the given input data & block indicates that the cipher will take a fixed-sized block as an input.
With DES, data is encrypted in 64-bit blocks, with a 56-bit key length, and with output ciphertext of 64 bits. DES has the same structure of a Feistel Cipher but without Initial Permutation (IP) and Inverse Initial Permutation. The DES encryption process can be further divided into the following stages:-
1. Key Generator Algorithm: The key generator passes through many steps to produce subkeys.

1.1 The key generator algorithm takes a 64-bit key as input. The input key number table from 1 to 64 is as follows:

1.2 Every eighth bit is ignored and produces 56 bits.

1.3 These 56 bits pass through a Permutation Choice one (PC-1) and displays as follows:

1.4 The output is separated into two 28 bits, C and D. The first 28 bits are called C0 (left part), and the last 28 bits are called D0.
1.5 At each round, a circular left shift is performed Ci−1 and Di−1 by 1 or 2 bits. See the table below:

1.6 Then Ci−1 and Di−1 in each round, pass through Permutation Choice two (PC-2) to produce 48-bits.

1.7 The Permutation Choice Two output in each round is used as input to the encryption algorithm.
2. Encryption Algorithm:
2.1 There are two inputs to the encryption algorithm:
a) Plaintext 64 bits b) Encryption key 48 bits.
2.2 The encryption algorithm also passes through many steps to produce a ciphertext. See the figure below:

2.3 The plaintext block 64 bits pass through an IP that the rearranged bits and produces the permuted input.
3. Initial Permutation:
3.1 IP takes the plaintext as input. The table consists of 64 bits numbered from 1 to 64:

3.2 Then the IP will be permuted input as 64 bits:

3.3 The Inverse Initial Permutation is:

3.4 The permuted input block is split into two halves, each being 32 bits. The first 32 bits are called L, and the last 32 bits are called R. Now, The F function will start the rest of all the steps.
3.5 Expand R 32 bits to 48 bits to fit the subkey by performing the Expansion permutation.
4. Expansion permutation (E):

Perform Exclusive-OR between the subkey and Expansion Permutation (E) on R.E(Ri-1)⊕ __K__i.5-The result of E(Ri-1)⊕ __K__i pass through a substitution function and produce 32 bits output. Substitution Function:
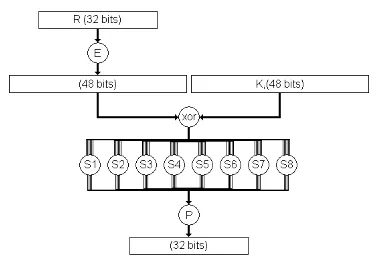
5. S-Box Permutation:
Substitution Function is rolled by S-Box. S-Box consists of 8 boxes, each of which accepts 6-bits as input and produces 4-bits output:
5.1 Break the result of E(Ri-1)⊕ __K__i into eight blocks, each containing 6 bits. These blocks are numbered from 1 to 8.
5.2 Each block will perform a substitution with S-Box with the same number:

5.3 The first and the last bits of each block together as 2-bit values indicate the number of rows in the same number S-Box.
5.4 The middle four bits of each block together as-bit value, indicating the number of columns in the same number S-Box.
5.5 The decimal value, selected by the row and the column, converts the to-bit value in all S-Boxes.
For Example: Suppose the first 6 bits of the result of E(Ri-1)⊕ __K__i = 010101. So, the input to S1 = 010101.The row value = 0 1 = 1 (decimal).The column value = 1010 = 10 (decimal).The decimal value will be 12 = 1100 (4-bit value).D- Combine results of each S-Box together 32 bits.6- The result of the substitution operation (output of S-Boxes) passes through a Permutation Function (P).

6. XOR & Swap:
At this point, the function F is finished.
6.1 Perform Exclusive-OR between the output of the Permutation Function(P) and Li−1. Then, put the result in Ri, and put Ri−1 inLi. The overall formulas for DES Encryption Algorithm: Li = Ri−1.Ri = Li−1 ⊕ F(Ri−1,__K__i).
6.2 Perform a 32-bit swap on the result of the final round. Then, perform Inverse Initial Permutation (IP−1) on the swapped data to produce the ciphertext 64 bits. Decryption Algorithm: The inputs to the decryption algorithm are ciphertext and subkey __K__i but in reverse order, start with __K__n then K(n−1), and so on until __K__1 in the last round.Note: You can use a DES Calculator https://github.com/Hamza-Megahed/des-calculator to study each round in detail.
DES Properties
DES being a block cipher satisfies the following beneficial properties which make it strong:-
- Avalanche Effect - When the input changes slightly (even by 1 bit), the output has a significant change (almost half of the output bits change).
- Completeness - When each bit of output depends upon many bits of the input.
DES Implementation
To implement DES, we use a security provider, for example, BouncyCastleProvider. The secret key that has to be used can either be user-defined or randomly generated using KeyGenerator from the javax.crypto package. Then we will add two methods for encryption and decryption, respectively, and later add a provider. Encryption will use cipher mode ENCRYPT_MODE, and decryption will use cipher mode DECRYPT_MODE. DES, being a symmetric block cipher, will use the same key to encrypt and decrypt. We will use the getAlgo() method to provide the algorithm to be used. You can refer to https://dzone.com/articles/security-algorithms-des-algorithm for a better understanding of the practical implementation.





